Input Data Logic Block
Description
The Input Data Block is a data source within a logic rule. The block can retrieve data from one of two sources:
- Trend Log data
- Constants
Functionality
This Logic Block sets the data source, sample interpolation and depending on the configuration, determines whether to transfer this value to working rules.
Name
The name is important. The first part of the name is the explanation of its role.
The second part of the name is tags, which are enclosed within curly braces. These tags are used by System Rule Discovery to find relevant Rule Templates. Kaizen uses HayStack tags. e.g. Hot Water Supply Temp {sensor, leaving, hot, water, temp} for a sensor of water temperature, specifically the hot water leaving the boiler or other heating equipment.
Use as default for Working Rule
When checked, this will copy the input from the Rule Template as a default to all of the Working Rules. It can still be edited at the Working Rule level. A default is good for items like:
- Room Temperature Set Point for buildings that generally have all rooms at the same temperature.
- Hours to trigger an insight on.
- Deadband for temperature accuracy.
- Occupancy when this is set for the whole building and not trended per system.
Defaults should not be used for items like:
- Motor Size when motors could be of different sizes
- Room Temperature as this is what you are trying to analyze.
- Occupancy when this is trended per system or per room.
Please note:
- You can use either of the input options of Trend Log Data or Constant Value as a default for working rules.
- The Community Library templates do not have Trend Log defaults but may have Constant value defaults.
- When using Trend Log Data as a default value, it gets automatically overwritten when the system’s auto-discovery is able to find the matching Trend Log in the TL Vault.
Input Mode
This Logic Block will accept input from Trend Logs or Constants. Trend Logs are trended values. Constants are entered in the block and can be easily edited/changed by the user at individual working rules. The heating dead band is an example of a constant. A well-controlled stable zone might have a dead band of 1 deg C (2 deg F) and a more dynamic zone might have 3 deg C (5 deg F).
Current Trend Log
When Input mode requires a Trend Log, it is specified here. This is the Trend Log to use when previewing the log flow. It can be set to being the default for Working Rule.
Data Interval
In order for any Logic Blocks to process samples, the input samples must be at the same time within the Logic Flow. Interpolation ensures that all samples are time-aligned and occur at the same frequency. e.g. 15 minute samples will be at 01:00:00, 01:15:00, 01:30:00, 01:45:00, 02:00:00 and not at random, different minutes or seconds. The user can choose the frequency of samples and the interpolation algorithm to use.
Frequency:
- options are: every 5 minutes, every 15 minutes, every 30 minutes, hourly, daily, weekly, monthly, annually
- allows the user to choose when samples will be output. 15 minutes is a good default. You may choose 5 minutes for calculations where you need more precision.
Interpolation Algorithm: The Interpolation algorithm determines how an input will be normalized about the time-axis.
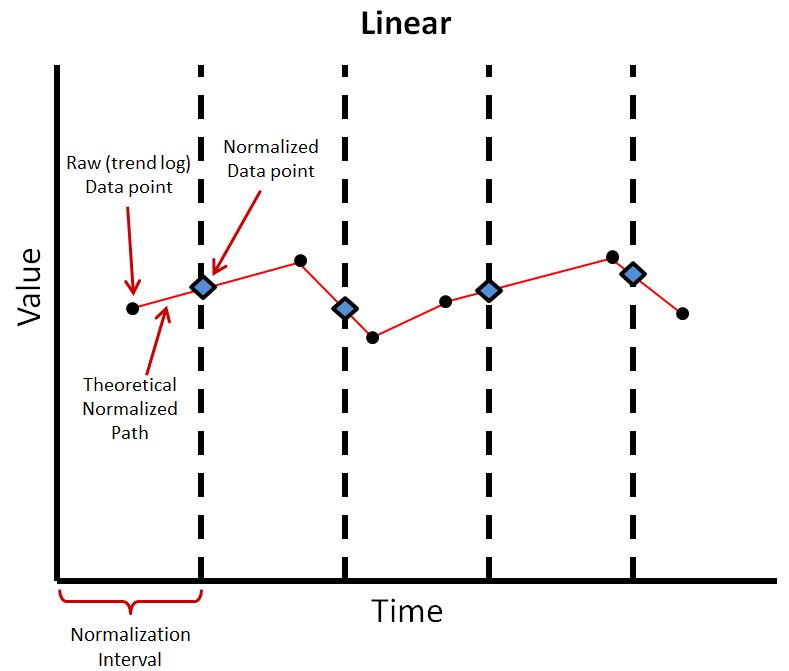
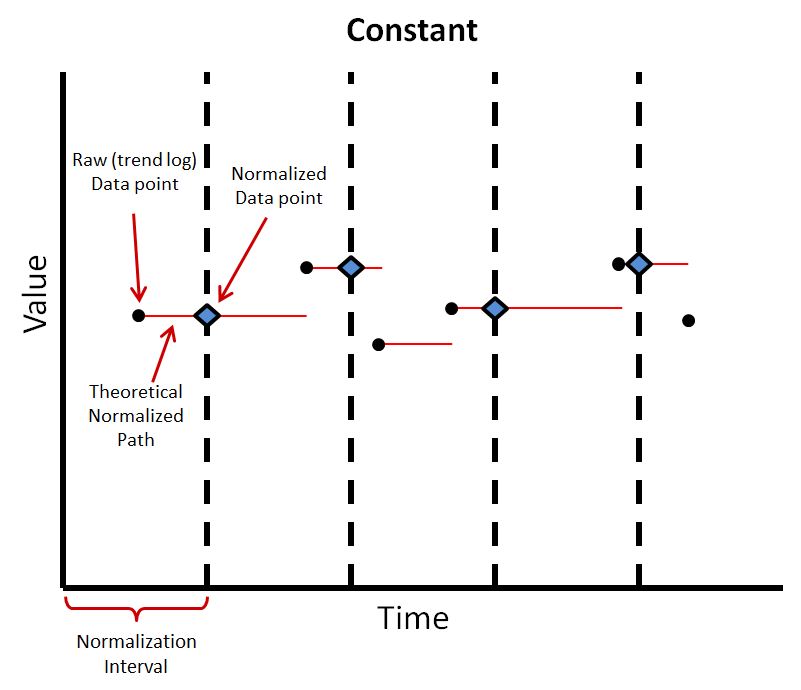
Normalizing Algorithms
There are two unique normalizing algorithms possible within this Logic BlockThe normalizing function includes outlier samples in the algorithm. The normalizing block will by default use the last data point available prior to the period of computation (date range) if at least one data point is available in the previous month. This capability ensures the correctness of COV Trend Logs and avoids using values that are no longer relevant (too old, more than one month) to perform the normalization.
The Constant normalizing algorithm takes the value of the last data point at the interval. This has the advantage of using the most recent data point and is not heavy in computation power. This also leaves nothing implied, as the normalized interval corresponds directly to the last data point. This is commonly used with binary object inputs and outputs, as then there are no unwanted fractional values. However, if there is more than one data point within an interval, which is likely the case, this does not take them into account.
The Linear normalization algorithm takes a linear interpolation at the interval between preceding and following data points. This allows the normalization to more accurately follow climbing and falling trends within the data series. This is the most common normalizing algorithm. However, this does not take into account more than one data point within an interval.